CMU Binary Bomb Lab Phase 2

Phase 2!

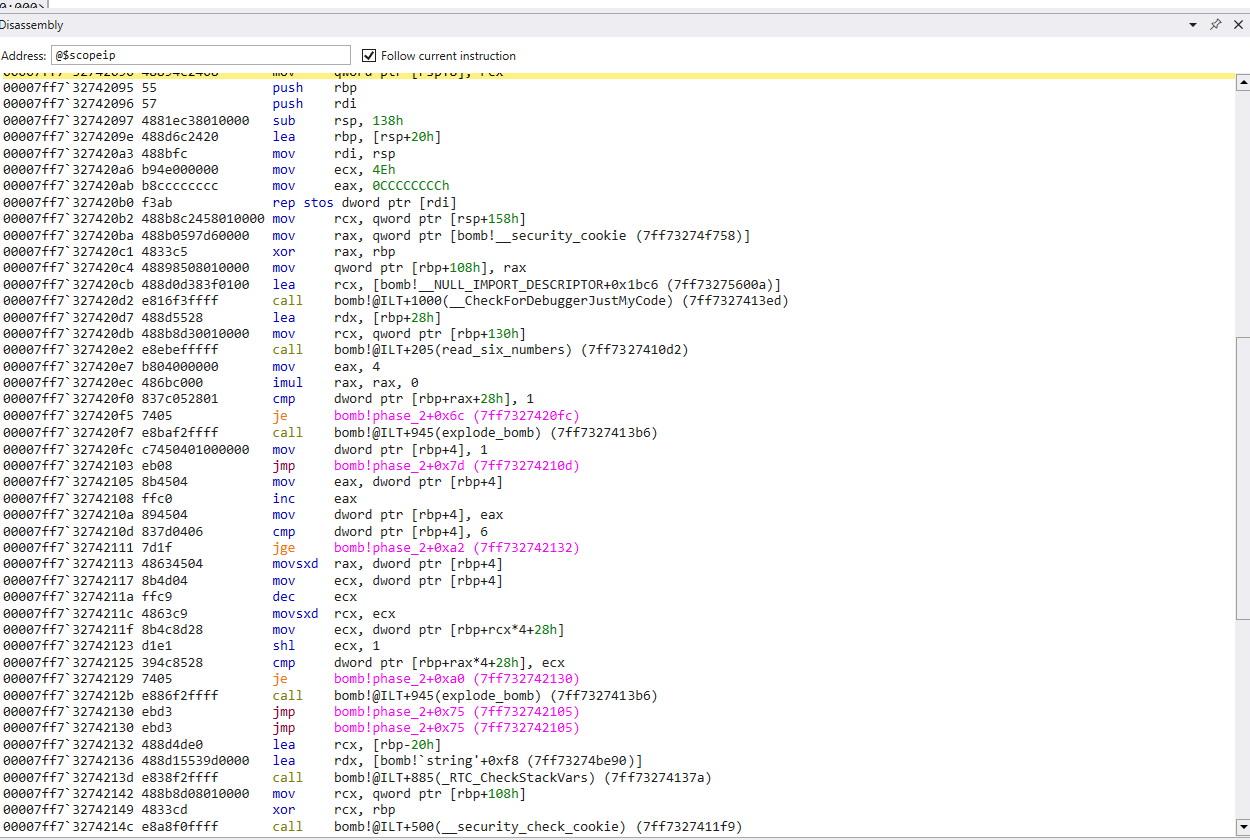
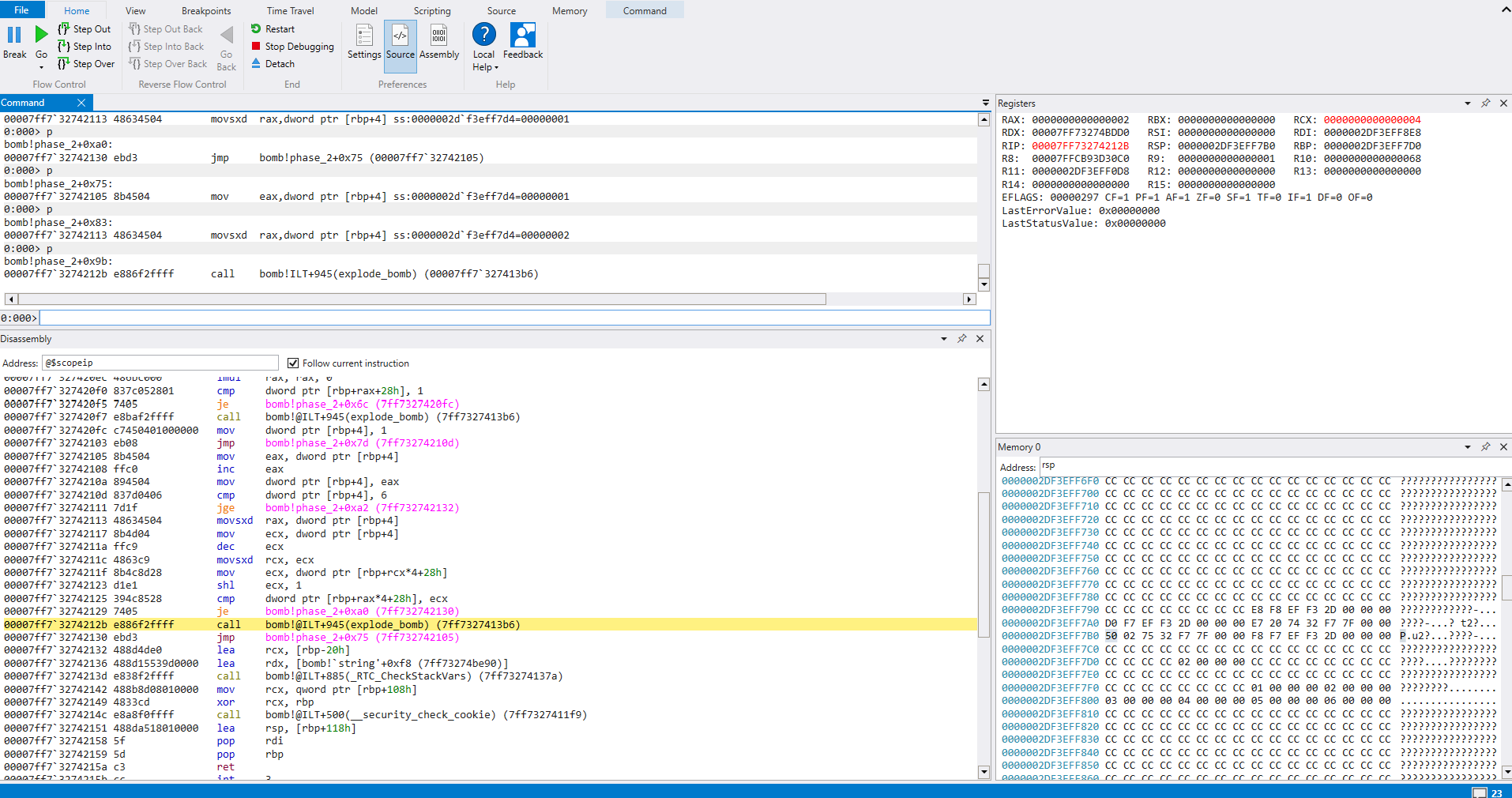
Upon stepping into the phase_2() function, we see the initial register saves, stack allocation, what appears to be some base pointer linking, along with some other familiar instructions.

phase_2

After the boilerplate code we have a function call to a new function

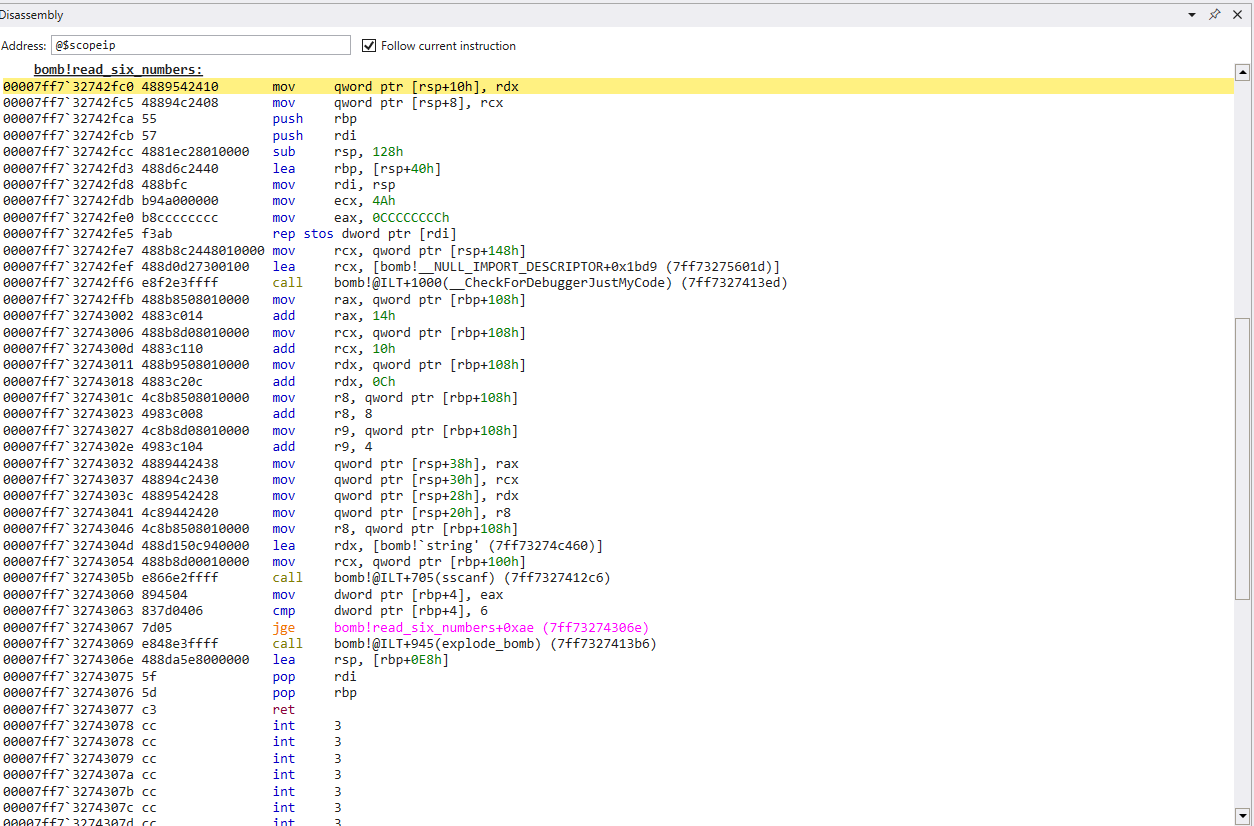
• read_six_numbers We can safely assume this function probably does what it says it does, but does it serve any other purpose? To find out, let’s take a look at the assembly code

read_six_numbers

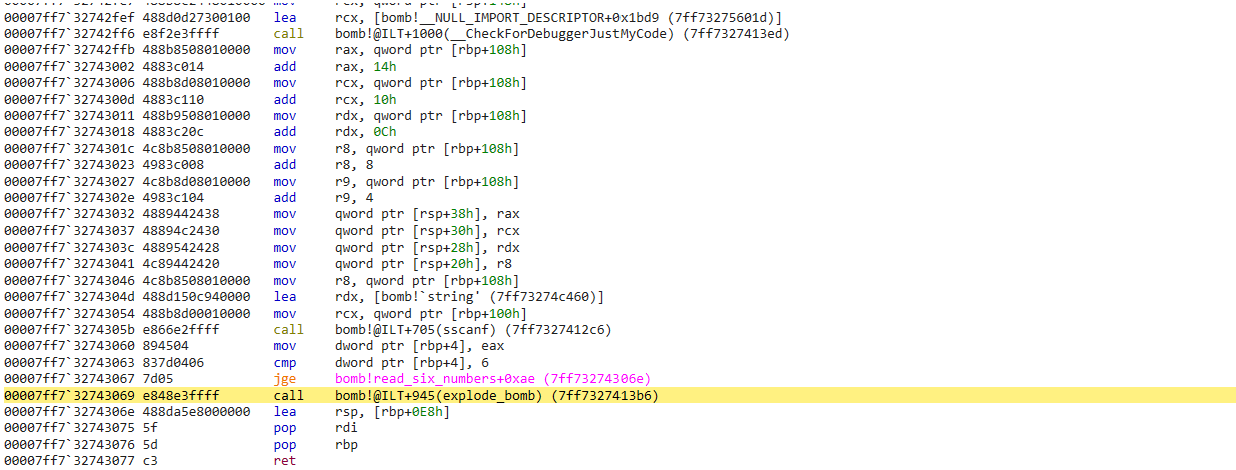
Looking at the only cmp instruction in read_six_numbers(), it looks like we are comparing the value from eax (moved to memory) with 6, and jumping over the explode_bomb() function if it is greater than or equal to. We can make an inference that this is what the code does, but what’s with all of the instructions? The surplus of add and mov makes me think those may be red herrings designed to waste our time.

Just before the call to sscanf(), we can see a string loaded to rdx and a pointer loaded to rcx. Based on Microsoft calling convention, I will assume rcx contains a pointer to our input, and rdx contains a format string, such as “%d”.

look at top window

Here we can confirm that our six numbers are being passed as a parameter to the function. Now let’s confirm the function is designed to verify we have passed in at least 6 digits.

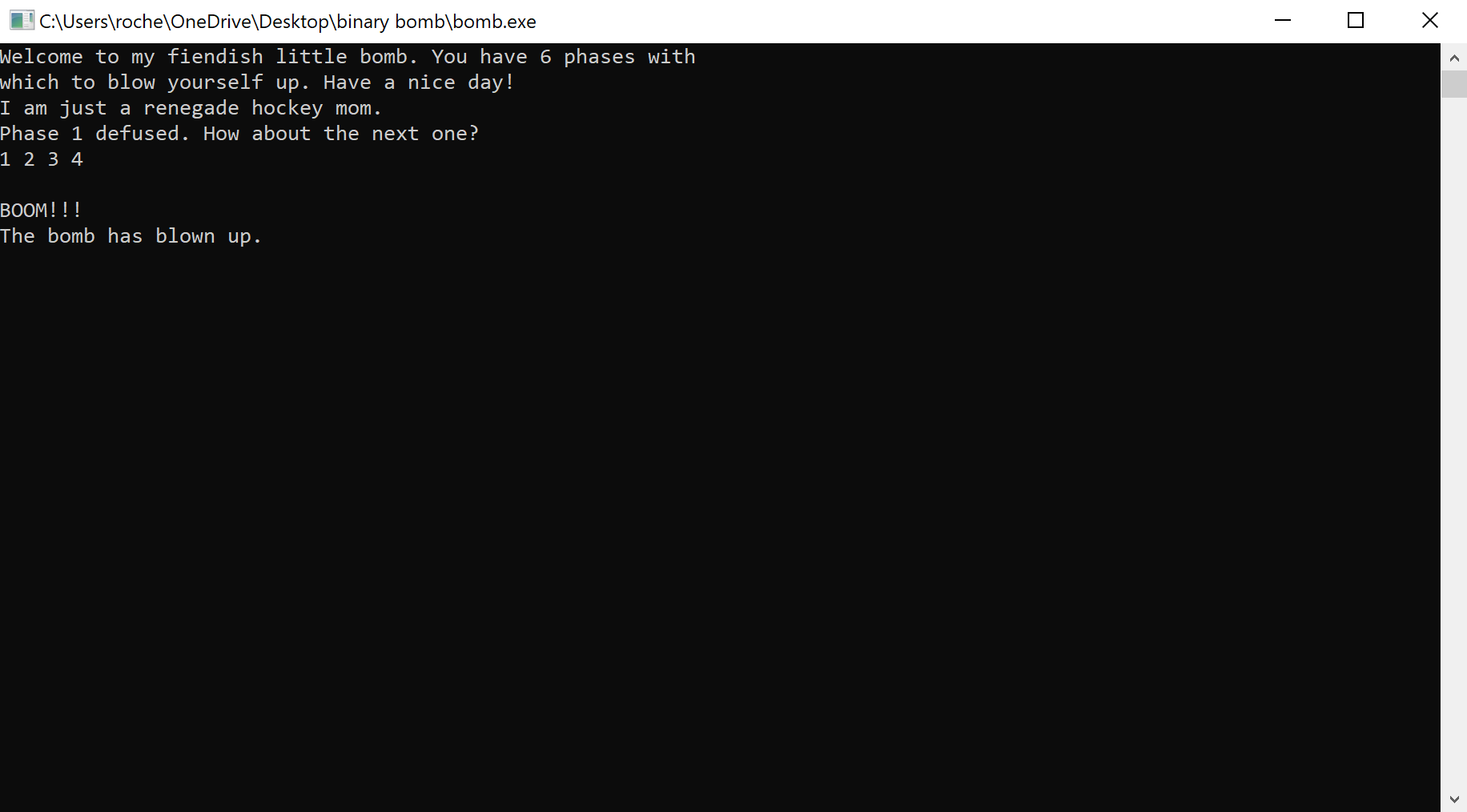
To confirm this is all read_six_strings() does, let’s try passing in less than 6 numbers and observe what happens.

jump not taken

boom

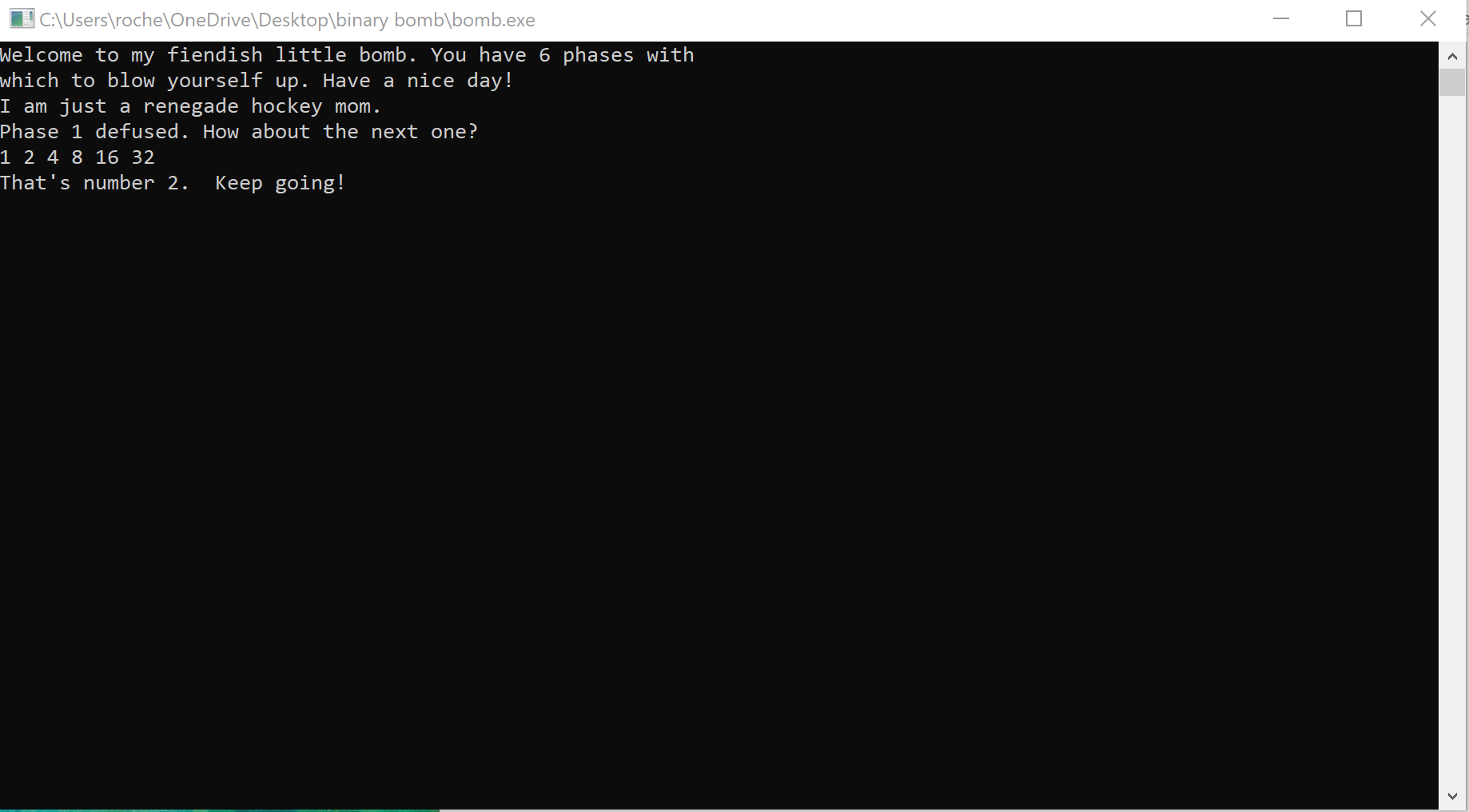
Our inference seems to be correct. So we know we have to pass in 6 numbers for our input, but what six numbers? To find out, we will have to take a closer look at phase_2(). Once we are past our input validation function, we see a few other interesting pieces of code

• We see a series of jumps and compares throughout the function
• We also see several calls to explode_bomb function.

So we know have to pass in 6 integers to survive the read_six_numbers(), let’s see what happens if we pass in 1 2 3 4 5 6.

Here is another view of the phase_2() function.

phase_2()

Just after the call to read_six_numbers(), we have this series of instructions

mov eax, 4
imul rax, rax, 0 //this zeros the register
cmp dword ptr [rbp+rax+28h], 1

If there is one pattern I’ve caught on to, espeically with Microsoft compiler, is that imul is often used to index some sort of array (or other structure). Earlier in the walk through we checked the values at [rbp+28h], and we confirmed that this was our input to be passed to read_six_numbers(). Since rax is now == 0, we can see this is an obvious comparison between our first integer passed and 1. Just below we have

je bomb! offset in func
call explode_bomb

If we do not take the jump we will explode. This confirms our first input should be 1 always.

Now what about the next 5 numbers?

mov eax, dword ptr[rbp+4]
inc eax
mov dword ptr[rbp+4], eax
cmp dword ptr[rbp+4], 6
jge ...

The above appears to take a value from memory, increment it, store it back in memory, and compare that with 6. This could be some control flow structure, maybe a for loop or while loop going to 6.

Next we see

movsxd rax, dword ptr[rbp+4]
mov ecx, dword ptr[rbp+4]
dec ecx
movsxd rcx, ecx
mov ecx, dword ptr[rbp+rcx*4+28h]
shl ecx, 1
cmp dword ptr[rbp+rax*4+28h]
je ...
call explode_bomb

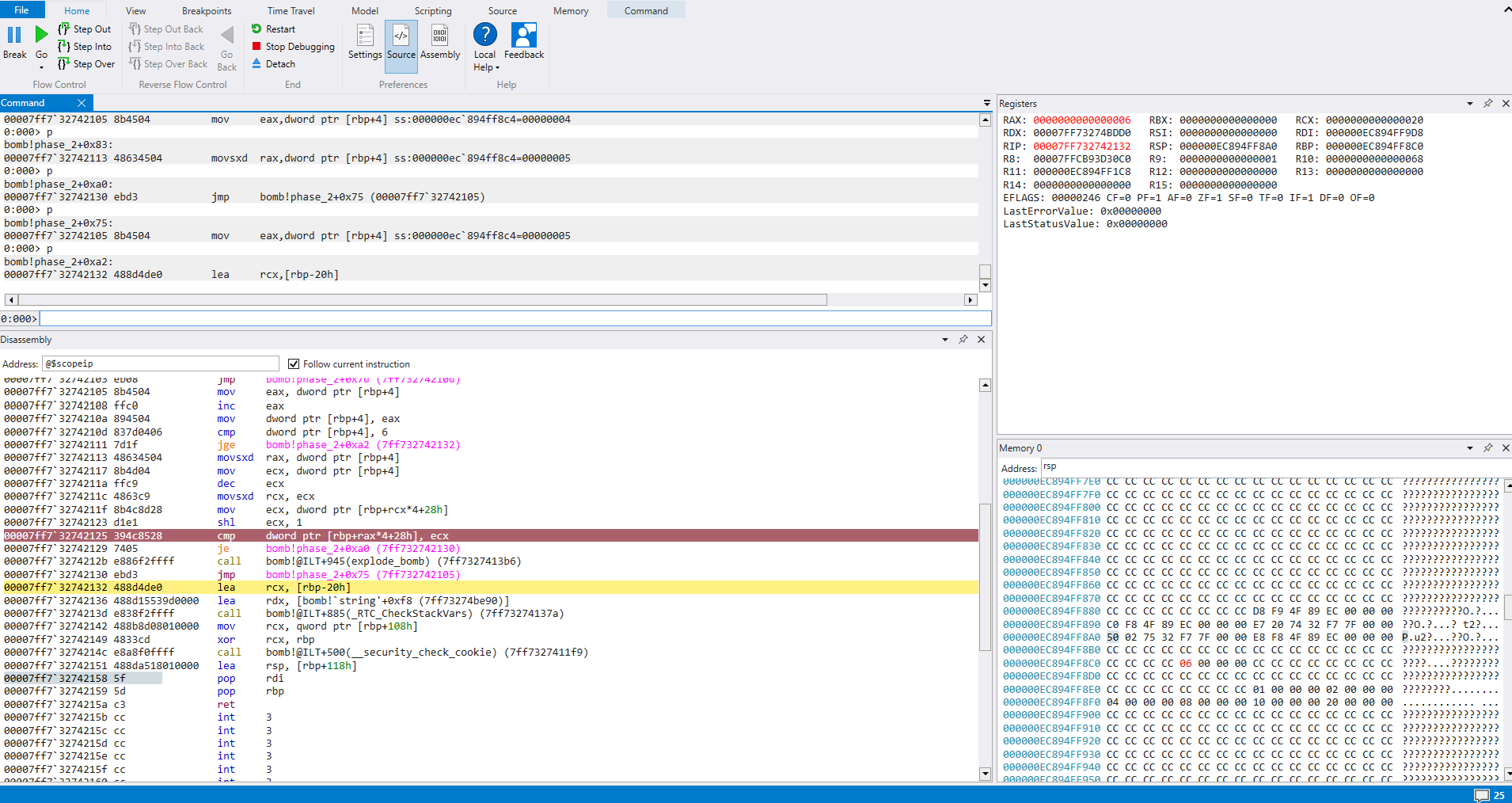
To sum this up, it looks like we take the value (possibly a counter) that we used in the previous comparison and move it into rax and ecx. ecx is decremented and moved with sign extension to rcx. It looks like we then access our input, but this time use rcx x 4 as the offset into the input. We then bitwise shift left, which is the equivalent of multiply by 2. Finally, we compare another value in our input ‘array’, but this time use rax x 4 as the offset into the input. rax is equal to ecx - 1 prior to the shift. If these are not equal we will explode. We can confirm this by checking a register view of our input from the above example

look at top right window

This confirms that rcx is being compared with rax x 2

The algorithm appears to be checking that (input[n-1]x2) == n, starting at input[1]

If this is the case, the expected input should be 1 2 4 8 16 32. Let’s give it a try.

success!

look at top right window

We can see that when rax is 0x6, rcx is 0x20, which is 32 decimal. rax was incremented again before our counter was compared with 6, so when it is 0x5, rcx is 32, therefore it certainly comparing input[n-1]x2 with input[n].

On to phase 3!