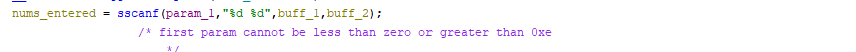CMU Binary Bomb Lab Phase 4

Phase 4!

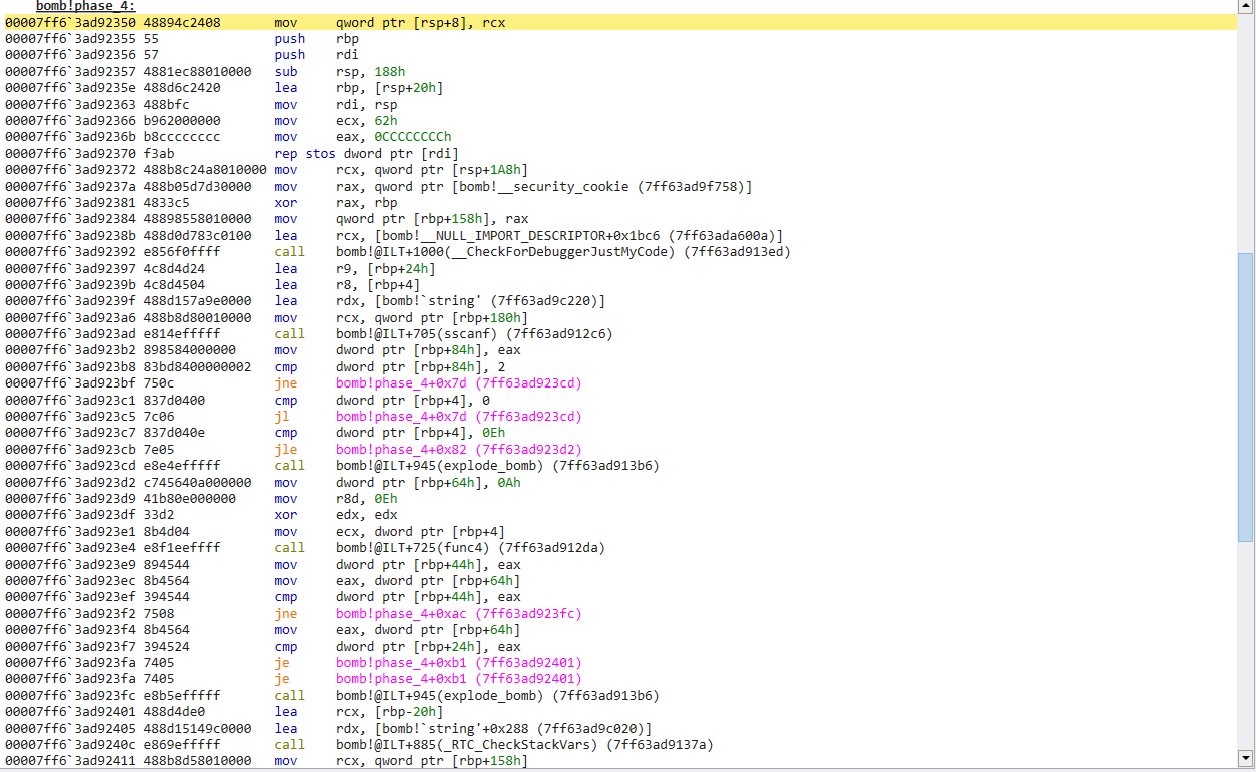
Here is a view of the phase_4() assembly code

For this phase, I decided to break out the reliable red dragon. Let’s throw this into Ghidra and start inspecting the this function.

Note: I did step through the decompiled code and change some variable names and add comments for readability purposes

phase_4() in Ghidra

First we are passing sscanf() pointer to our input, followed by our format string, followed by two buffers to store the extracted integers.

sscanf view in ghidra

Looking at our first ‘if’ statement, there is 3 separate checks, any of which will result in an explosion. These are

• nums_entered != 2
• buff_1[0] < 0
• 0xe < buff_1[0]

Based on the constraints, we must pass in 2 integers, our first input cannot be less than zero or greater than e (14).

Seems easy enough. Here comes the fun.

Just before the second ‘if’ statement, we have a few declarations

a = 10;
func4_ret = func4(buff_1[0], 0, 0xe);

Followed by the second ‘if’ in phase_4() which checks that

• func4_ret != a
• buff_2[0] != a

According to the second set of constraints, both func4_ret and buff_2[0] must == 10. This seems pretty straightforward, we just need to ensure that func4_ret == 10

The first call to func4() is here

func4_ret = func4(buff_1[0], 0, 0xe);

The parameters are

• First integer we input to the program
• second is zero
• third is E (14)

Let’s take a look into func4() to see how to get the return value we want

We assign a local variable before proceeding with the ‘if-else’

local_f4 = x + (e-x)/2

If we evaluate this using the parameters passed first, we get

local_f4 = 0 +(14-0)/2 == 7

Next we have the conditional statement

if (first_input < local_f4) {
	iVarl = func4(first_input, x, local_f4 + -1);
	local_f4 = iVarl+local_f4;
} else if (local_f4 < first_input) {
	iVarl = func4(first_input, local_f4+1, e);
	local_f4 = iVarl+local_f4;
}

which will always check if our input is greater than or less than local_f4 on the first pass through. As you probably noticed, this function makes recursive calls to itself in either case we take.

To cut straight to it, local_f4 will always be 7 on the first pass, and we need to return from this function with the value 10, meaning we need a recursive call that will result in a return value of 3.

I will unashamedly admit this took me a while tracing through recursive calls by hand, but if we pass in an initial value of 3 we can trigger this by:

(I will plug in values rather than variables for readability)

local_f4 = 0 + (14-0)/2 == 7
if (3 < 7) {
	iVarl = func4(3, x, 6);
	local_f4 = 7+iVarl
}

This first call is ready to return 7, but it is waiting for the recursive branches to return. Here is the recursive call step-through

local_f4 = 0 + (6-0)/2 == 3
if (3<3){
...
} else if (3<3){
...
}
//input and local_f4 are equal, so we skip both conditionals
return local_f4

Which will ultimately result in us returning back to phase_4() with the value of 10 just as we needed.

Looking back at our last conditional statement,

Since a == 10, we can see above that our input of ‘3 10’ should successfully avoid all of the ‘code mines’, if you will.

Let’s give it a shot

On to phase 5!