CMU Binary Bomb Lab Phase 5
Phase 5!
This is the longest phase so far. I tried my best to explain my approach in a way it hopefully makes sense.
We are now on phase 5 of the infamous CMU Binary Bomb challenge.
Let’s begin!
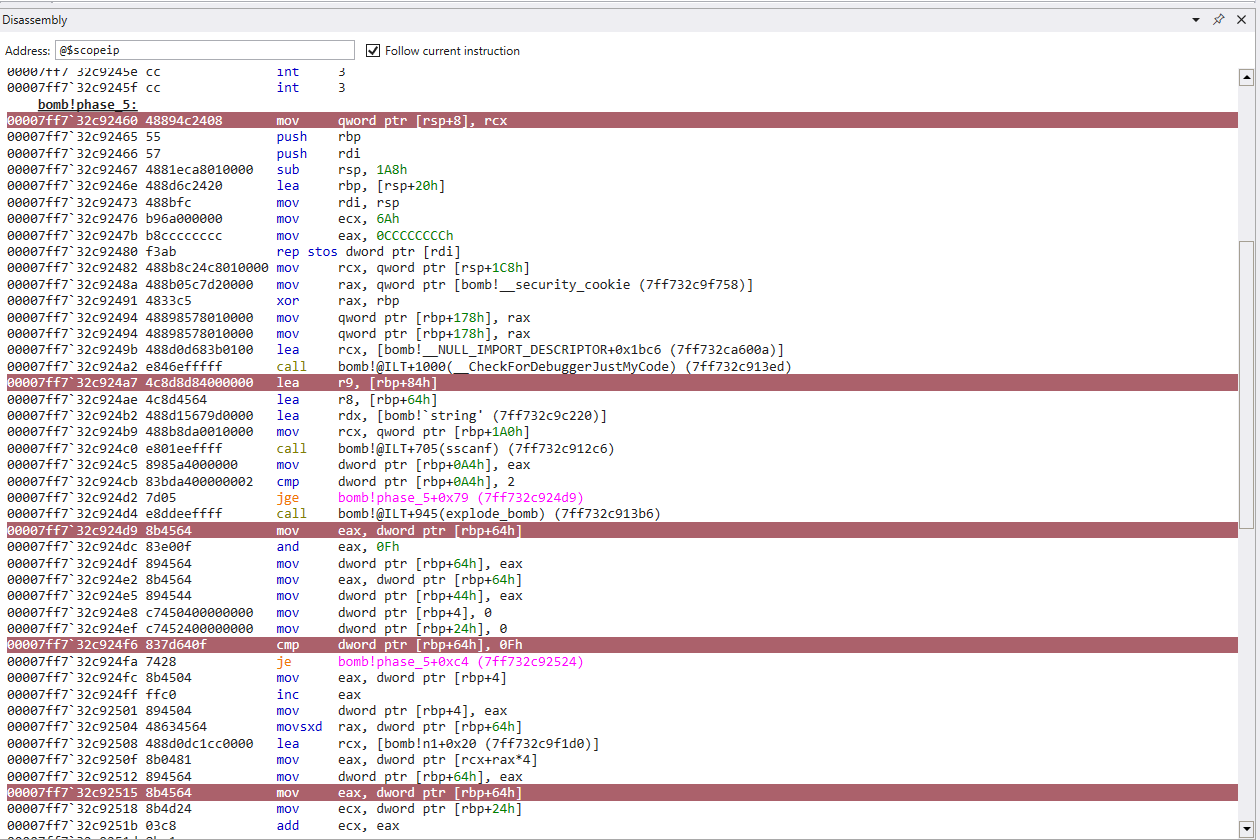
Looking at the assembly, we can immediately start dissecting the relevant information
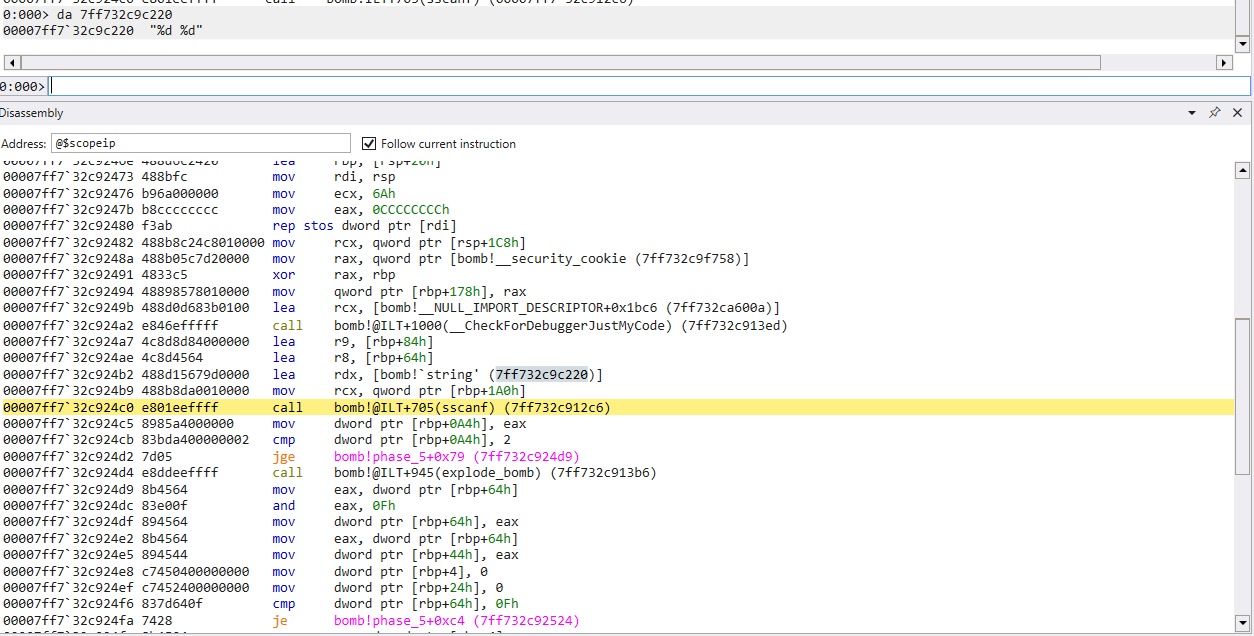
There is a call to sscanf(), let’s find out what kind of input this function is expecting
Let’s take the same steps as the last few phases, by analyzing the memory being loaded into rdx before we call sscanf()
We can see here that phase_5() is expecting 2 integers
Now to find out what the two integers are we need to look at the logic
1
2
3
4
5
6
7
8
9
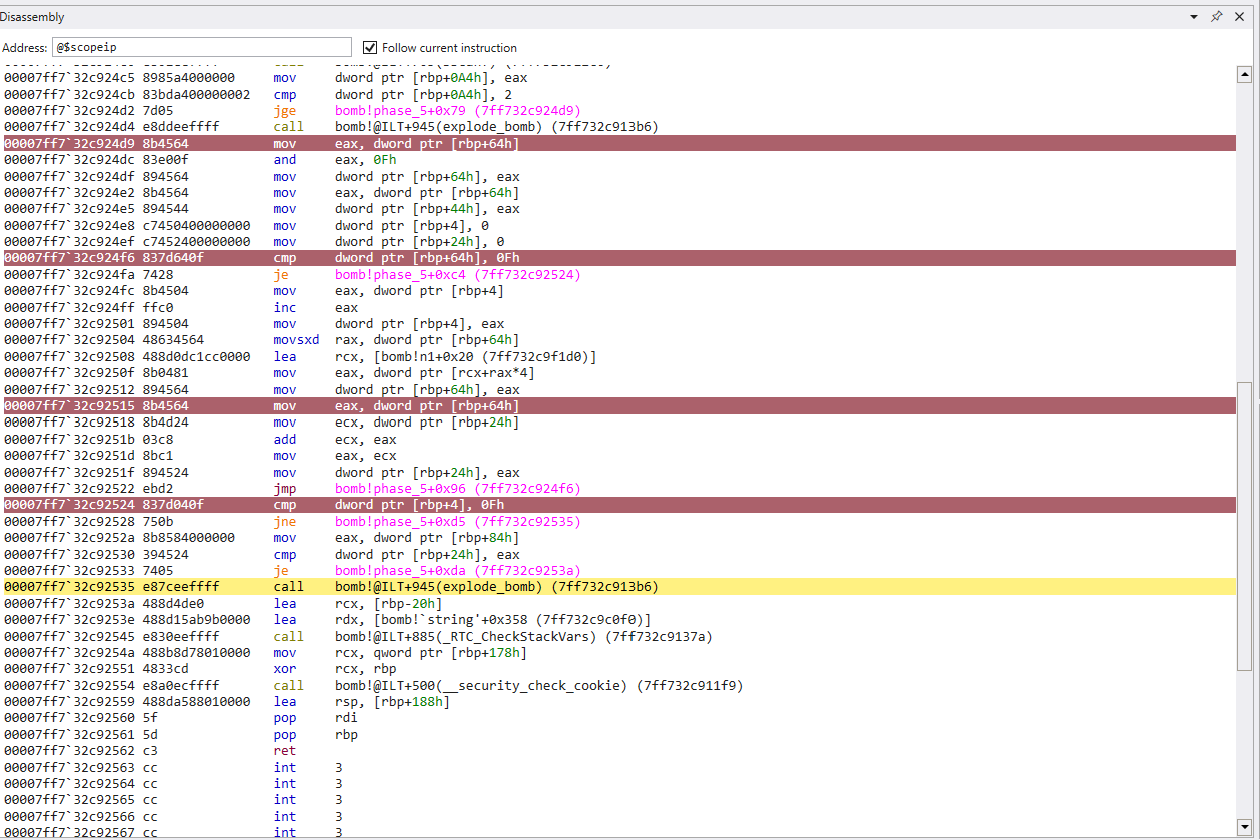
mov eax, dword ptr [rbp+64h]
and eax, 0Fh
mov dword ptr [rbp+64h]
mov eax, dword ptr [rbp+64h]
mov dword ptr [rbp+44h], eax
mov dword ptr [rbp+4], 0
mov dword ptr [rbp+24h], 0
cmp dword ptr [rbp+64h], 0Fh
je ...
To make things short, it looks like we load our first input from memory, initialize some variables to 0, and compare our first input with 0xF. If these are a match, we take a jump to a place further down in the function
If our first input does not match 0xF, we will continue
1
2
3
4
5
6
7
8
9
10
11
12
mov eax, dword ptr [rbp+4]
inc eax
mov dword ptr [rbp+4], eax
movsxd rax, dword ptr [rbp+64h]
lea rcx, memory[7ff732c0f1d0]
mov eax, dword ptr [rcx+rax*4]
mov dword ptr [rbp+64h], eax
mov eax, dword ptr [rbp+64h]
mov ecx, dword ptr [rbp+24h]
add ecx, eax
mov eax, ecx
mov dword ptr [rbp+24h], eax
It seems like we have some control flow based on the move from memory into eax, followed by increment and a move back into memory. It’s probably halfway safe to assume this is a counter of some sort.
Based on the pointer notation, it seems we are indexing a value from an array and moving it into eax, and then moving it into the memory of our initial input1.
This is added with the value stored in [rbp+24h], and moved back into [rbp+24h]. This looks like a x = x+y for each iteration of the loop. Let’s put this into Ghidra and take a closer look, as we need to find out what is being indexed in memory
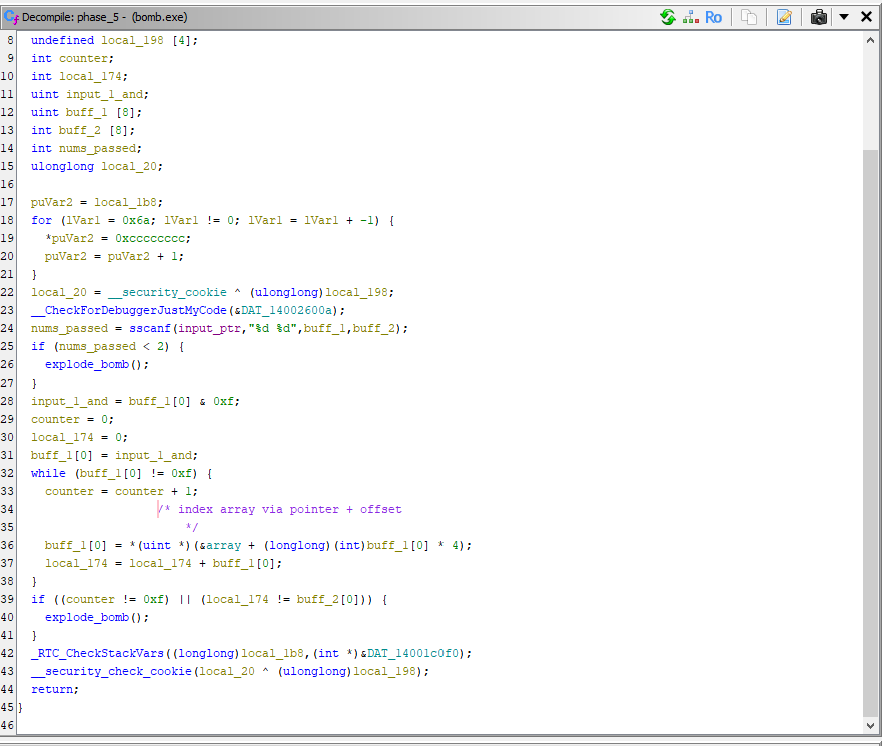
Note: I’ve changed some variable names and added comments for readbility
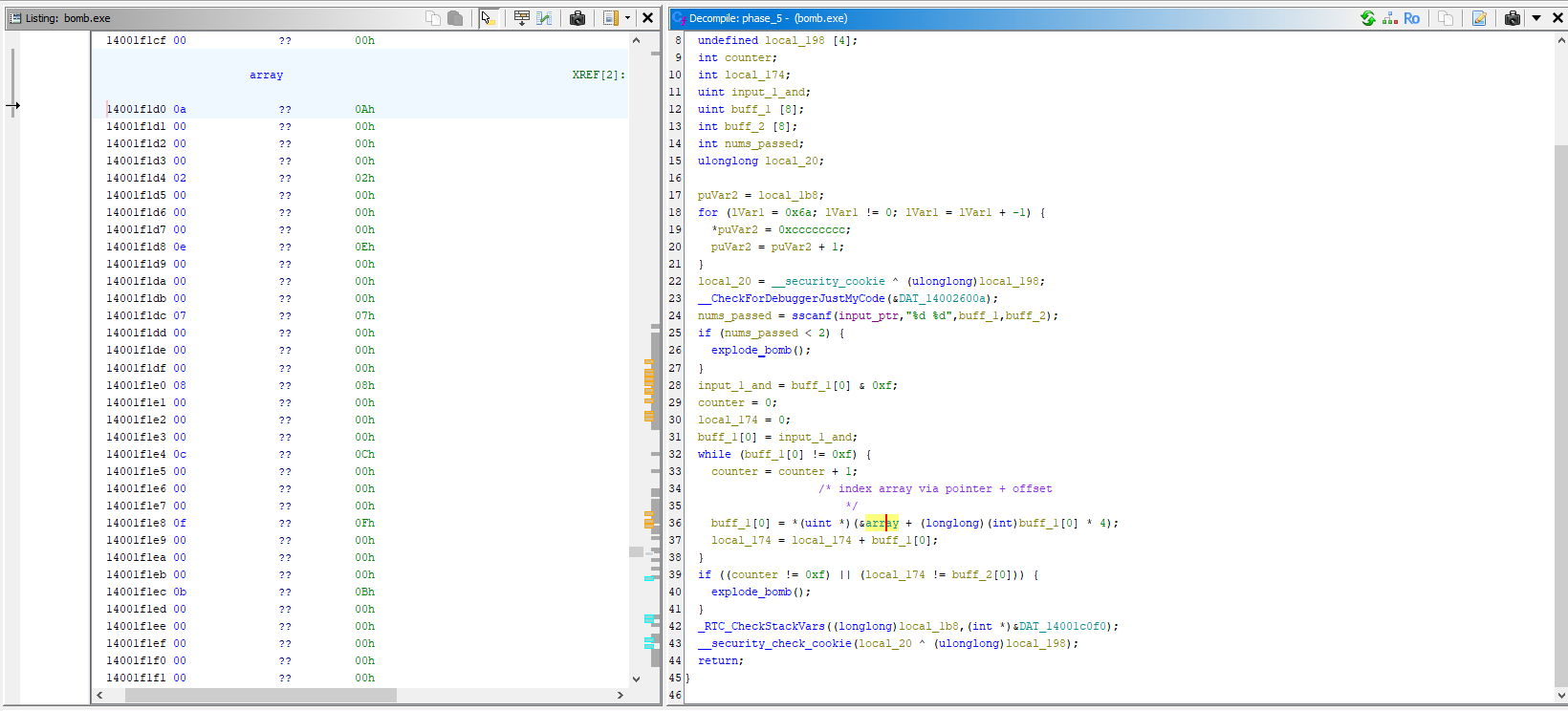
Here I have a decompiled view of what is going on, now let’s dissect it
At the top of the function we have
1
2
uint buff_1[8];
uint buff_2[8];
which are the buffers sscanf() reads our input into
Next we have a while loop
1
2
3
4
5
while (buff_1[0] != 0xf) {
counter = counter+1;
buff_1[0] = *(*uint)(&array+(longlong)(int)buff_1[0]*4);
local_174 = local_174 + buff_1[0];
}
Note: moving forward, I am going to refer to buff_1[0] as input1. Same for the second input.
Based on the above loop, it will loop until input1 == 0xf, and for every iteration, our counter is incremented by 1. input1 is the reassigned to a value in memory
1
buff_1[0] = *(*uint)(&array+(longlong)(int)buff_1[0]*4);
This is clearly indexing from the start of the array + (input1x4), but what is this array? Let’s follow it in memory and take a look
From what I can tell, this array is randomized integers, which are spaced 4 bytes apart in memory.
Why can’t we just avoid this array and while loop altogether? Let’s just pass in 0xF as input1 and never even enter this while loop contraption
Well, to avoid exploding we must satisfy the last ‘if’ statement
1
2
3
if ((counter != 0xf) || (local_174 != buff_2[0])){
explode_bomb();
}
Meaning the code must iterate exactly 15 times through the while loop since
1
counter = 0;
at the start of the loop, and increments by 1 each iteration
1
counter = counter + 1;
You may see where this is going, but there are essentially two conditions we must satisfy to pass this case. We need to iterate exactly 15 times to satisfy the counter check, and on the 15th iteration we need
1
2
buff_1[0] = *(*uint)(&array+(longlong)(int)buff_1[0]*4);
to be assigned the value of 0xF to exit the while loop.
Once we satisfy these conditions, we can then pass the
1
local_174 != buff_2[0]
case by checking the memory at that location when we successfully exit the loop. That will give us our second expected input.
So, how can we make this loop run exactly 15 times and land exactly on an index holding 0xF to store in input1?
I did this the old-fashioned way, by creating a map tracing what index leads to F, and working backwards from there to find the 15th value.
Let’s look at the array again
The formula for calculating input1 in the while loop above is essentially a pointer to the start of array + input1*4, which indexes the array using pointer notation.
For example, if we pass in 0 for input1, our offset is 0 and input1 would be the first value of the array (0Ah).
Next calculation would be array + 40, which would lead us to the 40th byte of this array.
The map looks like this
1
2
input1 = 3 -> 7 -> B -> D -> 9 -> 4 -> 8 -> 0 -> A -> 1 -> 2 -> E -> 6 -> F
counter =0 1 2 3 4 5 6 7 8 9 10 11 12 13
To pass this case, counter should == 15 when input1 == 15 (F) , so based on our above map, we need to find an input that can direct us to 3 for the second value of the map
3 is located at index array[48], so if this calculation is correct, initial input of 5 should take us to array[20] which is 12, which should then direct us to array[48] which is 3, and proceed with the rest of the stream above, hopefully ending with input1 == F and count == F
The correct stream should be
1
2
3
input1 = 5 -> 12 -> 3 -> 7 -> B -> D -> 9 -> 4 -> 8 -> 0 -> A -> 1 -> 2 -> E -> 6 -> F
counter =0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
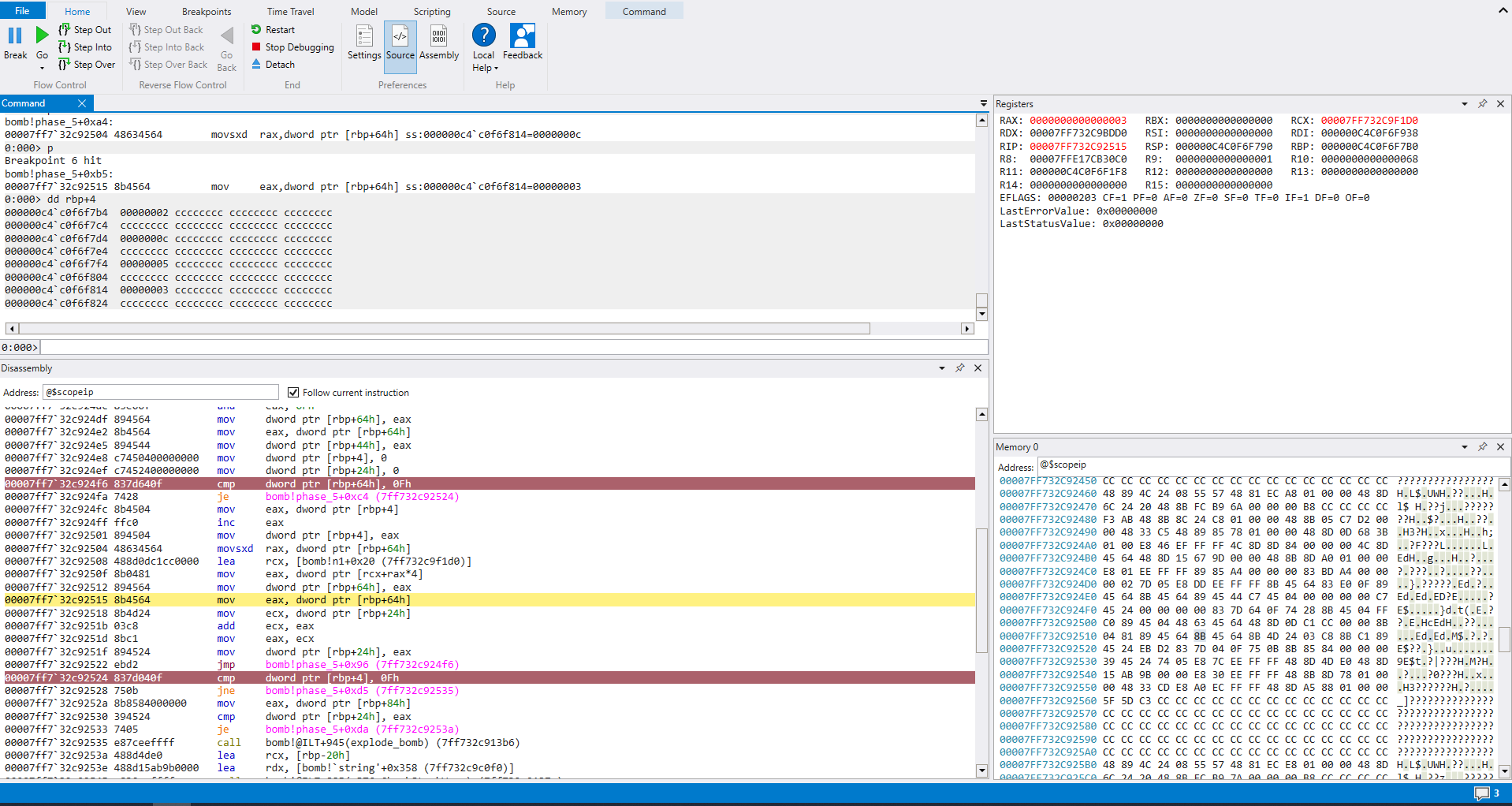
Let’s pass in our input of 5 x and watch counter and input1 change
Looking at the register view window, we see RAX == 3, and printing the memory storing the counter at [rbp+4], we can see it is 2.
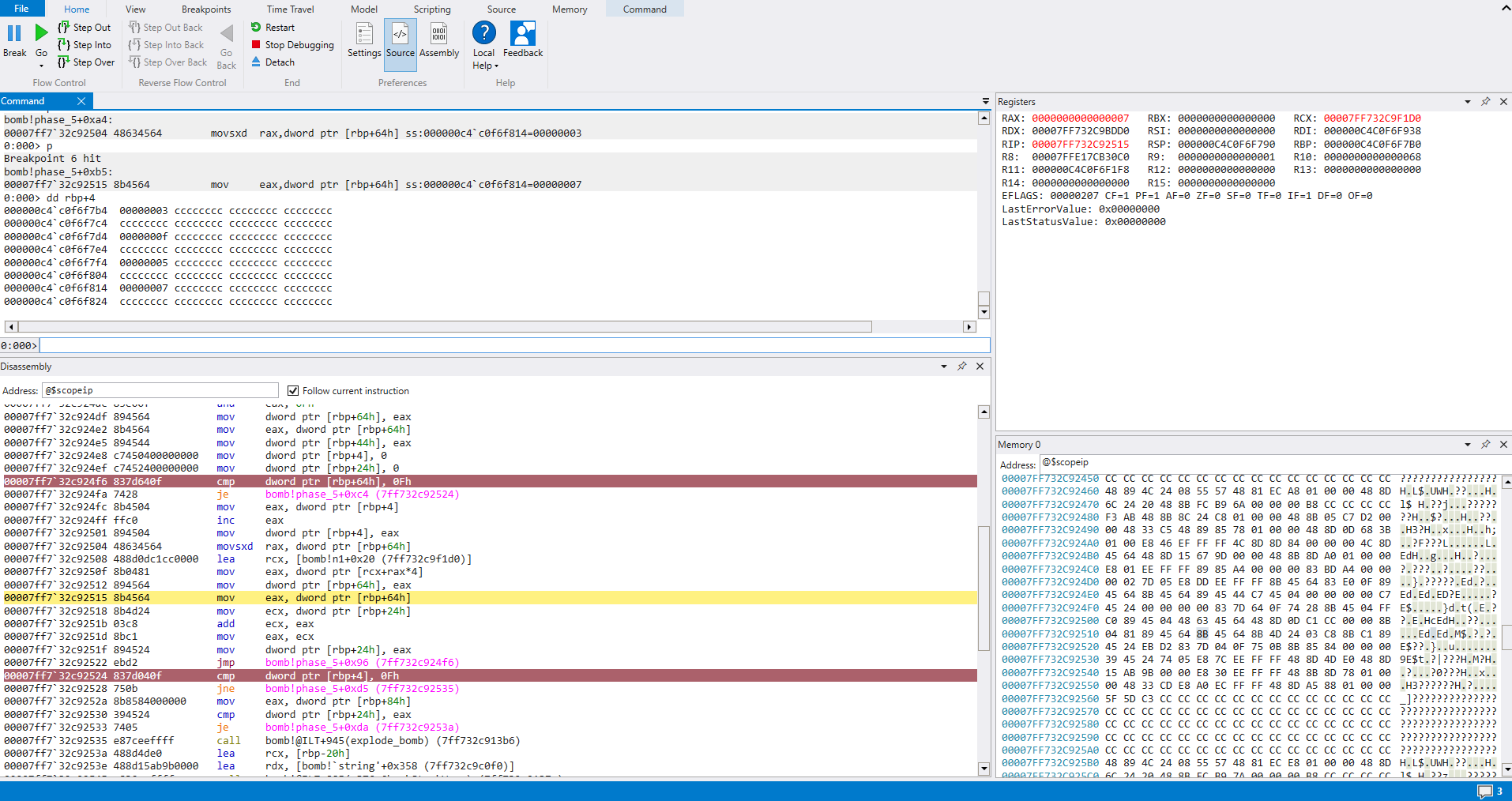
Next up should be input1 == 7, with counter == 3
This looks to be correct, we just need to confirm this exits the while loop and passes the first check.
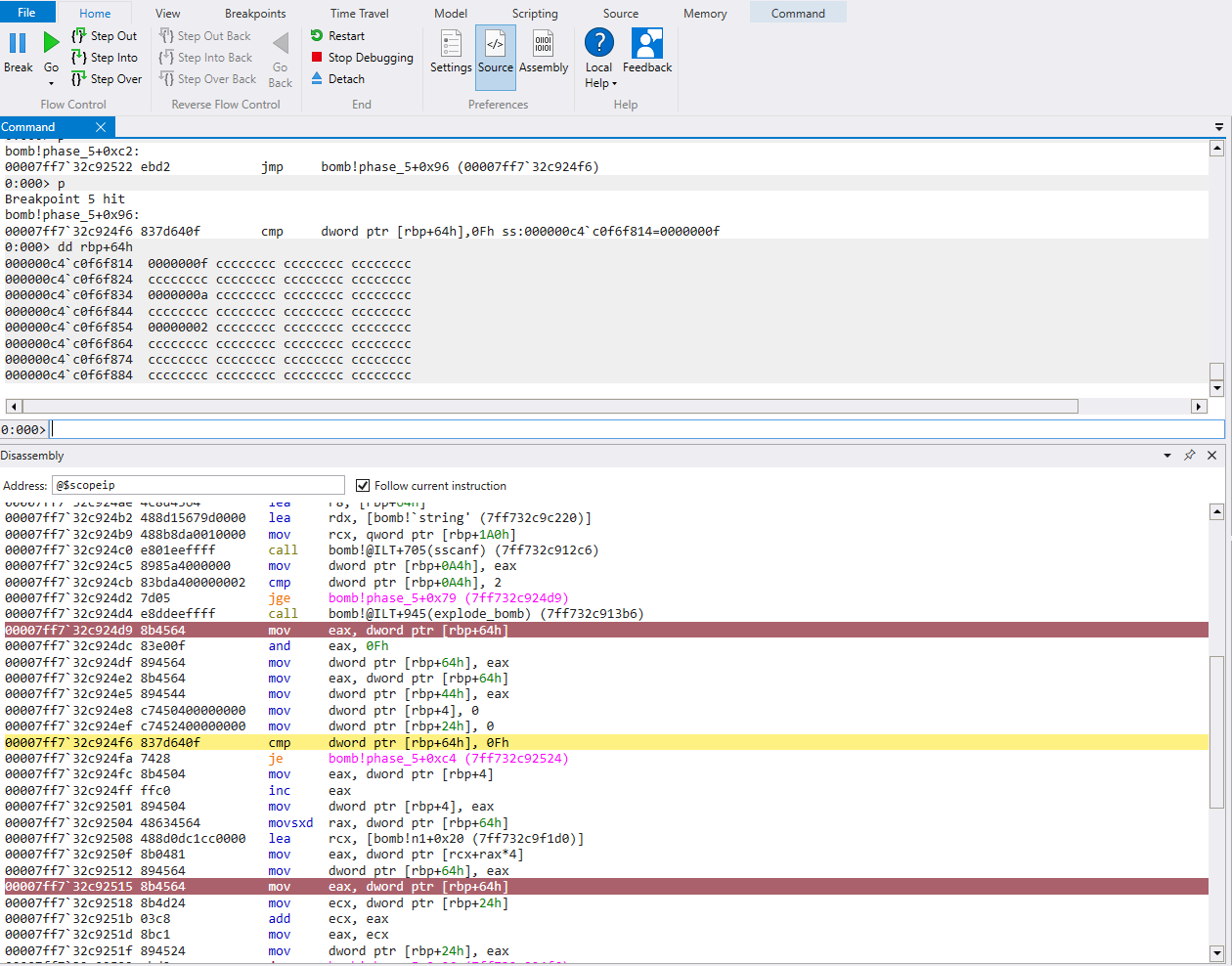
Let’s confirm input1 == 0xF passes when exiting the loop
Great!
Let’s confirm counter == 0xF passes
Wonderful.
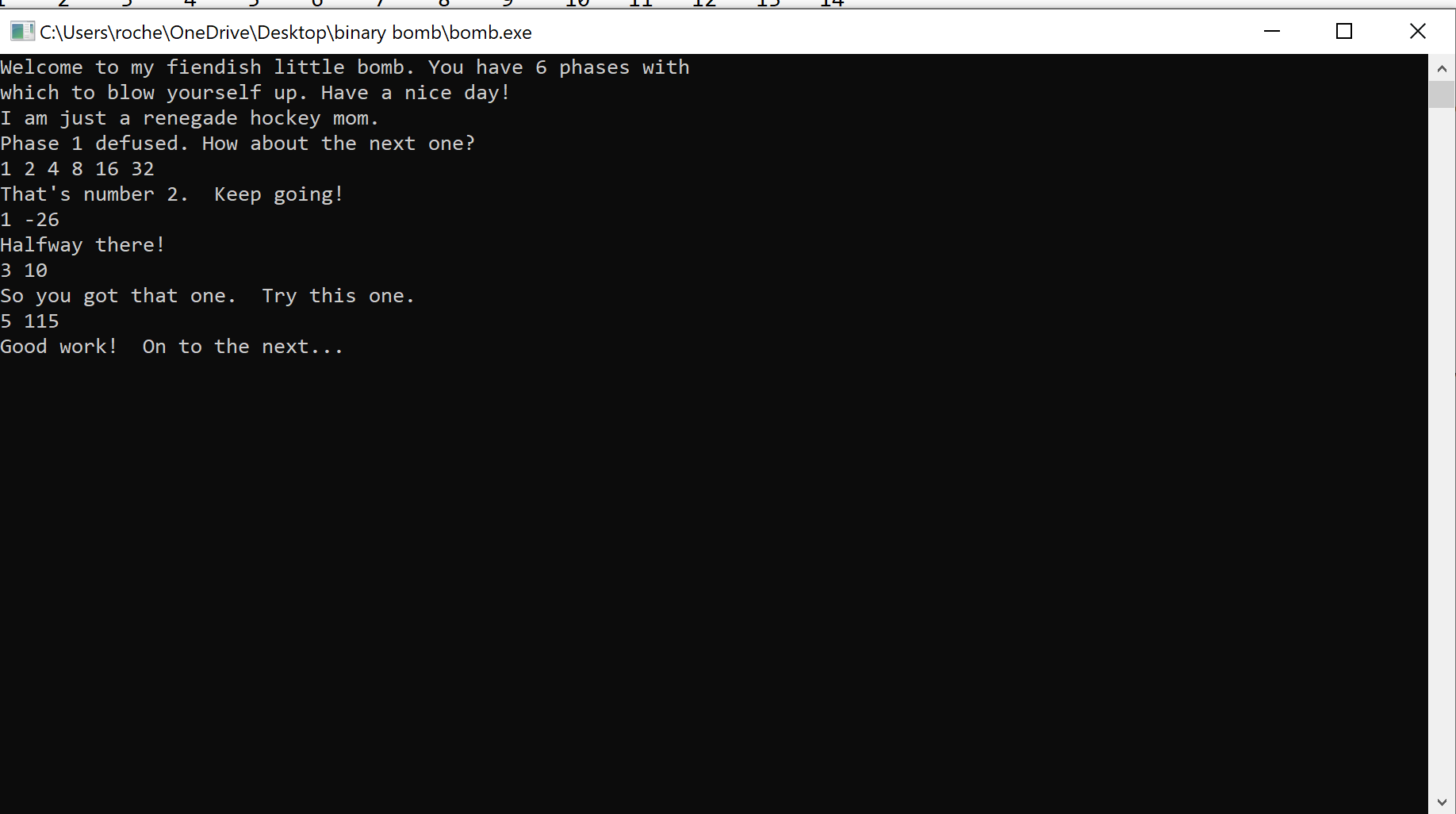
Now that we know input1 == 5 is the first key, the last step is to find out what input2 should be. This can be done by viewing the memory of local_174 after exiting the loop, since that’s what input2 should be.
Dumping the memory, we find our initial input of ‘10’ at [rbp+84h] is being compared with ‘0x73’ at, or 115 in decimal at [rbp+24h].
Thus, our solution should be ‘5 115’. Let’s give it a shot
On to the last Phase! (hopefully)